Flashbots的MEV竞价是最佳的吗？_以太坊

Flashbots的MEV竞价是最佳的吗？

由 Flashbots 开辟的MEV竞价服务项目已遭受了矿工们的热烈欢迎，那麼这类竞价是不是最佳的呢？

注：全文作者是斯坦福学校电气专业博士研究生Guillermo Angeris，placeholder 研究者Alex Evans及其Gauntlet创办人Tarun Chitra。

在包（Bundle）分配问题中，矿工遭遇着固定不动总数的交易，而她们要将这种交易包含在给出的区块中，除此之外，矿工还能够挑选在该区块中包含（或清除）什么包（Bundle）。矿工根据将每一个包（Bundle）包含在区块中获得盈利，殊不知，包（Bundle）具备许多务必要考虑到的分派约束。在本文中，大家得出了一个简易的整数金额线性规划问题难题（ILP）公式计算，并给予了一些基本上的拓展。

矿工可获取使用价值（MEV）这一专业术语，指的是矿工依据交易排列可得到的一切经济利润。在区块链等区块链技术系统软件中，客户根据点到点的gossip互联网向矿工递交一组交易和花费。而矿工们会搜集这种交易，并将他们分次成一个彻底井然有序的编码序列，随后由大部分矿工认证并接纳做为下一个区块。

殊不知，在许多区块链中（比如以太币），矿工可挑选要包含的交易集及其递交交易的次序。

假如一名矿工递交一笔具备经济发展实际意义的交易，她们能够对交易再次排列以保证她们的交易最先实行，这也被称作抢先交易（front running）。自打MEV这一定义被明确提出至今，早已发生了许多涉及到闪电贷、借款及其三明治进攻的新式 MEV 方式。MEV意味着了一种使用价值获取方式，而客户没法根据简易地改动其交易竟价个人行为来清除它。

公平公正（Fairness）。从理论上讲，MEV 很有可能造成 区块链的共识不稳定，并很有可能驱使客户在预估交易花费以外付款附加的花费来解决交易。这也引出来了许多科学研究，而这种科学研究的关键是确保交易排列及包含层面的“公平公正”。而公平公正优化算法试着应用密码算法方式 ，比如对交易排列或未处理交易情况的時间锁服务承诺（time-locked commitments），以强制性根据時间的“公平公正”确保。

MEV竞价。或是，有一些科学研究工作中说明，MEV是区块链特有的，它没法根据单纯的密码算法方法删掉。这一系列工作中合理地说明，对比用密码算法方法删掉MEV，矿工和客户共享资源MEV盈利将造成 平稳的平衡。

在这个由 Flashbots 开辟的全球中，“探索者”尝试寻找交易的最好次序，随后竞投由矿工以特殊次序实行的“包”交易。这类竞价根据 MEV 竞拍开展协商——即参加者想要在链下竞拍中往矿工付款附加的优先选择竞价。因而，MEV竞价是更火爆的，而且这类方法在2021 年为矿工造就了超出 7 亿美金的附加收益。

最优性（Optimality）。殊不知，一个当然要问的基础理论难题是，这类竞价是不是最佳的呢？现阶段，Flashbots竞价根据应用约束求得器处理背包问题(Knapsack problem)来合理地实行交易包（bundle）。可是从理论上讲，大家应当期待类似整数金额线性规划问题 (ILP) 的解决方法是“最佳”的吗？应当怎样叙述最优性？因为 MEV 是依据全部财产的可获取使用价值来界定的，因而一切最佳定义都在于一切一组交易移动和包（bundle）可完成的较大盈利。

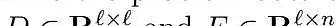
汇总（Summary）。在这篇短毕业论文中，大家得出了在单独区块中包含交易包（bundle）的最佳ILP的第一个宣布叙述。大家的叙述偏重于 MEV 的三种实际操作方式，包含抢先交易（front running）、跟随交易（back running）及其三明治交易（sandwiching）。大家假定结合实际应用的精准gas仿真模拟方式 是做为预备处理流程实行的，它将分配问题（找寻最佳包分派的难题）与恰当可能单独包（bundle）盈利的难题解耦。大家的公式计算能够非常容易用高級描述语言（比如CVXPY）开展提升并结合实际应用。

界定

在这里节內容中，大家最先来叙述一下这篇毕业论文中应用的基本上界定。

交易（Transaction）：矿工一般从一系列的交易逐渐，大家把这种交易写出一些结合T（将包含在区块中）。这种交易由区块链的客户给予，他们能够是Uniswap 或Curve的swap交易、借款或推测机升级等交易。

包（Bundle）：矿工还接纳很多由客户递交的包（Bundle），说白了包（Bundle）是一个含有关系交易的实际操作（action，大家稍候界定），每一个包（Bundle）还包含了一些竞价，比如，客户想要付款要多少钱才可以将其包（Bundle）包含在区块中。矿工能够决策区块中包含什么包（Bundle）及其交易。而矿工从包（Bundle）中得到的盈利，相当于区块中包含的每个竞价的总数。

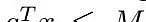
实际操作（action）：从之前逐渐，每一个包（Bundle）都将一个实际操作（action）与一笔交易（t ∈ T）关联。很有可能的实际操作（action）是：抢先交易t（在t以前实行一笔交易），跟随交易（在 t 以后立即执行一笔交易），及其三明治交易（在t前后左右都实行一笔交易）。

针对给出的交易 t ∈ T，要不是开展三明治交易t，要不是开展抢先交易及其跟随交易t。比如，如果有三个包（Bundle）与交易t关系，在其中一个在t以后开展跟随交易，一个实行抢先交易，另一个实行三明治交易，那麼矿工能够挑选包含抢先交易包（Bundle）和跟随交易包（Bundle），或是是三明治交易包（Bundle），但不可以与此同时包含这两个种类。

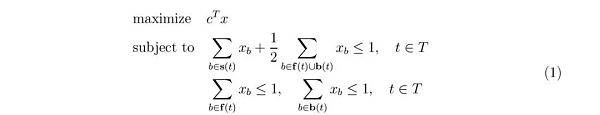
大家把这三个实际操作的室内空间称之为A。如今我们可以非常容易地将包（Bundle）界定为与交易t ∈ T 关联的实际操作（a ∈ A），而它会有一个竞价额度（ p > 0）。即包（Bundle）是一个三元组(a,t, p) ∈ A × T × R ，全部包（Bundle）的结合将由 B ⊆ A × T × R 得出。

利益最大化（Profit maximization）。剩余的难题是：矿工如何选择什么交易包含在她们的区块中，以完成利益最大化？在下一节中，大家将展现这一难题可描述为一个简易的整数金额线性规划问题难题（ILP），而其一般可根据现代计算机在有效的時间内处理。

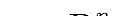
大家将利益最大化难题描述为整数金额线性规划问题 (ILP)，大家将其称之为包（Bundle）分配问题。

设定涵数。为便捷考虑，大家将撰写界定下列涵数。这儿，t ∈ T是一笔交易，而B是全部包（Bundle）的结合。

大家将s（t）界定为与三明治交易t关系的包（Bundle）结合：

相近地，f（t）是与t关联的抢先交易，b（t）是与t关联的跟随交易。大家假定 B 由 b = 1, 2, ... 数据库索引，在其中 n 是建议的包（Bundle）的总数。

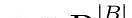
难题阐述：将包（Bundle）分配问题写出整数金额线性规划问题难题的一种简易方式 以下：

是提升自变量，假如当今区块中应包含包（Bundle）b，则xb为1，不然为0。难题数据信息是

，这是一个空间向量，促使 cb ≥ 0 是矿工在她们的区块中包含包（Bundle）b所得到的盈利，而T是要包含在这里区块中的交易集（不包括包（Bundle））。

规范方式。难题 (1) 可以用引流矩阵表达方式写的更简约一些。因此，大家将界定m = |T|，交易数量，及其引流矩阵

为：

针对每单交易t∈ T移动和包（bundle）b ∈ B，应用这种新的界定，难题（1）可以用下列方法撰写：

在其中1是适度层面的全1空间向量，而

是提升自变量。

表述。我们可以将总体目标和约束表述以下。总体目标

只是是包含在区块中的包（bundle）得出的盈利总数。第一个约束代表着区块中数最多包含一个三明治包（bundle），或是区块中数最多包含2个抢先交易或跟随交易 t的包（bundle）。第二个约束代表着针对每单交易t，数最多包含一个抢先交易包（bundle），及其数最多包含一个跟随交易包（bundle），而最后一个约束是将x的内容约束为布尔值。

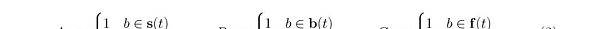
放比较宽松。一般来说，除开十分小的案例以外，难题 (1) 很有可能难以处理，由于x的内容有布尔运算约束。可是，在很多具体情况下，将布尔运算约束放开为界限约束（box constraint，即 0 ≤ x ≤ 1），历经一些简易的舍入计划方案后，能够造成有效的具体特性及其有效的解决方法。一般来说，这一比较宽松难题的最好总体目标，自始至终是矿工很有可能得到的较大盈利的限制，而一切舍入计划方案都是会得出一个低限。这能够用于得出所建议的包（bundle）分派的最优水平的一个界线。比如，假如放开后的盈利为1.2 ETH，而拟议分派的盈利为1 ETH，则拟议分派的最优性数最多为 1.2/1 − 1 = 20%。也就是说，数最多可将建议的分派提升20%。

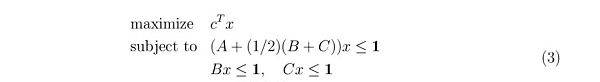
难题（1）几个简易但十分有效的拓展。

包（bundle）约束。比如，客户很有可能期待特定好多个包（bundle），这种包（bundle）务必由矿工一次性所有包含，或是压根不包含。我们可以把它写出包（bundle）Bi ⊆ B的非空子集。针对 i = 1, 。. . , ℓ，假如Bi中包含一切一个包（bundle），则矿工务必包含包（bundle）Bi的全部非空子集。

新的优化问题由下边的公式计算得出：

在其中提升自变量是

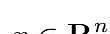
，而难题数据信息是在(2) 中界定的引流矩阵

和引流矩阵

也就是说，D是一个对角矩阵，其顶角内容是结合Bi的尺寸，而 F 是一个引流矩阵，促使 (Fx)i 得出了 Bi 时要包含在区块中的包（bundle）的总数。约束Fx=Dy简易地表明，针对每一个很有可能的i，要不包含全部| Bi | 包（bundle），要不只包含0个包（bundle）。

gas限定。另一种很有可能（且比较简单）的拓展，是在优化问题上包含总gas约束。比如，当包含在区块里时，每一个包（bundle）b ∈ B很有可能应用一些最很多的gas（由gb ≥ 0得出）。我们可以非常容易地额外约束，即包（bundle）应用的较大 gas 总产量不超过交易（但不包括 包（bundle））实行后剩下的 gas 量；即

，在其中 M ≥ 0 是剩下的gas量。大家注意到，这可能是一个难以得到有效限定的总数，由于当区块中包含包（bundle）时，交易应用的gas很有可能会产生前所未有的巨大改变。有别的很有可能的方式 来开展测算，但大家没有这儿探讨他们。

在这篇毕业论文中，大家给予了一个简易但十分通用性的公式计算，它能够用以处理矿工利益最大化包（bundle）分派的难题。尽管该难题一般是NP问题，但大家猜疑大部分整数金额线性规划问题求得器（乃至线性规划问题松驰）在具体情况下很有可能有非常好的主要表现。

由 Flashbots 开辟的MEV竞价服务项目已遭受了矿工们的热烈欢迎，那麼这类竞价是不是最佳的呢？

注：全文作者是斯坦福学校电气专业博士研究生Guillermo Angeris，placeholder 研究者Alex Evans及其Gauntlet创办人Tarun Chitra。

大家把这三个实际操作的室内空间称之为A。如今我们可以非常容易地将包（Bundle）界定为与交易t ∈ T 关联的实际操作（a ∈ A），而它会有一个竞价额度（

动态性 | 降维安全实验室变成CloudFlare全世界地区代理:据官方公告，降维安全实验室已变成CloudFlare云服务器全世界地区代理，CloudFlare给予不限量DDoS安全防护，服务承诺网址不黑客攻击退出。[2019/2/19]

非洲数据货币交易企业Bitflash提起诉讼11家银行:在今年的1月创立的非洲数据货币交易企业Bitflash LTD近日向特拉维夫地域法院起诉11家银行，规定被告银行为其开户。Bitflash控告这种银行产生垄断性同盟，回绝为其开户的个人行为违背了法律条款。Bitflash被拒绝服务攻击的缘故取决于虚拟货币不符一些银行的开户标准，可是在其中一些银行却为市场竞争企业给予有关银行服务项目。[2018/2/2

标签：

区块链热门资讯